问题
单项选择题
设矩阵A=(α1，α2，α3，α4)是5×4矩阵，η1＝(1，2，-1，3)T，η2＝(3，2，5，3)T是齐次线性方程组Ax=0的基础解系．下列命题中错误的命题是
(A) α1，α2，α3线性相关． (B) α3，α4线性无关．
(C) α4可由α1，α3线性表示． (D) α2可由α3，α4线性表示．
答案
参考答案：C
解析： A是5×4矩阵，齐次方程组Ax=0的基础解系是两个向量，故n-r(A)=2，即r(A)=r(α1，α2，α3，α4)=2．故(A)必正确．
由Aη1=0，Aη2=0可得
α1+2α2-α3+3α4=0，3α1+2α2+5α3+3α3=0
两式分别相减、相加可得
α1+3a3=0，2α1+2α2+2α3+3α4=0
如果α3，α4线性相关，则α4=kα3，又α1=-3α3，从而
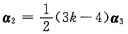与r(α1，α2，α3，α4)=2相矛盾，故(B)正确．
因为α1=-3α3，且α3，α4线性无关．故α4必不能由α1，α3线性表出，即(C)不正确．
因为α3，α4线性无关，α2，α3，α4线性相关，所以α2必可由α3，α4线性表出．