问题
单项选择题
设函数F(u,v)具有一阶连续偏导数,且
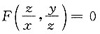 确定隐函数z=z(x,y),则
确定隐函数z=z(x,y),则
(A) x2F’1z’y+z2F’2z’x=0. (B) x2F’2z’x+z2F’1z’y=0.
(C) x2F’1z’y-z2F’2z’x=0. (D) x2F’2z’x-z2F’1z’y=0.
答案
参考答案:B
解析: 求全微分可得
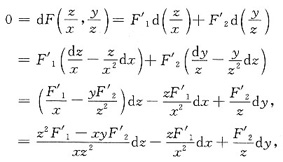
从而
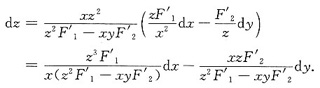
由此即知
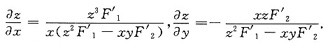
不难发现
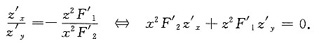
应选(B).
