问题
问答题
设a，b是满足b＞a＞1的两个常数，确定p与q的值使得
(Ⅰ)当x∈[a，b]时px+q≥lnx；
(Ⅱ)
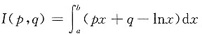取得最小值．
答案
参考答案：[解] 首先要使I(p，q)最小，直线y=px+q必须与曲线y=lnx相切，设切点为(t，lnt)，则t满足方程组
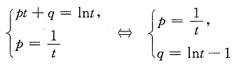
于是
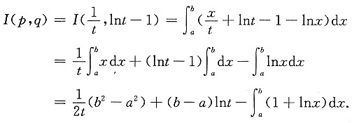
由于
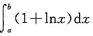是一个常数，因此I(p，q)与函数
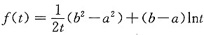有相同的最小值点．计算可得
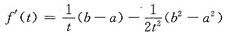
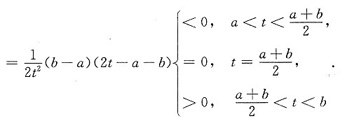
由此即得I(p，q)当
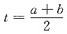时取得最小值，即当
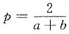且
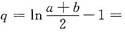ln(a+b)-ln2-1时I(p，q)最小．