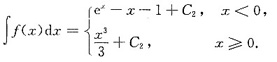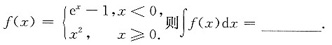
参考答案：

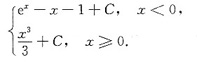
解析： 因函数f(x)在(-∞，+∞)上连续，取定x₀，作从x₀到x的变限定积分

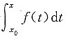就是函数f(x)的一个原函数，从而函数f(x)的不定积分为

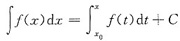，其中C是一个任意常数．
为计算方便起见，在本题中应取x₀为函数f(x)的分段点，即应设x₀=0．于是f(x)的一个原函数是

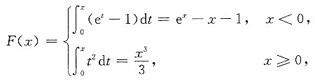
而f(x)的不定积分是

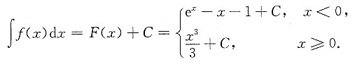
其中C是一个任意常数．
[注意] f(x)的不定积分不能写成

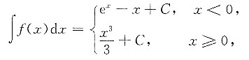
这是因为所得函数在分段点x=0处不连续，从而，在x=0点处不可导．f(x)的不定积分也不能写成

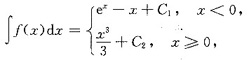
这是因为所得函数中包含了两个任意常数C₁和C₂．不过，如果取C₁和C₂的值使上述函数在x=0点连续，即取C₁+1=C₂，这个函数就变成为f(x)的不定积分了，即