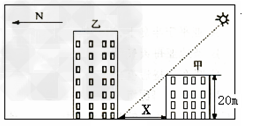
问题
问答题
二次型
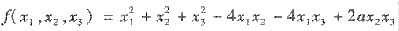，经过正交变换化为标准形：
，
(1)求a，t的值．
(2)求所用的正交变换X=PY．
答案
参考答案：二次型矩阵为[*]；其标准形矩阵为[*]，由于二次型经正交变换化为标准形，故A与A不仅合同而且相似，由相似矩阵有相同的迹知1+1+1=3+3+t，故t=-3．
由[*]，故a=-2(二重)．
对λ=3，由(3E-A)X=0得A的两个线性无关特征向量：
X1=(1，-1，0)T；X2=(1，0，-1)T
对λ=-3，由(-3E-A)X=0得A的特征向量：
X3=(1，1，1)T．
因为λ=3是二重根，对X1，X2正交化，得
β1=X1=(1，-1，0)T，
[*]
单位化得[*]
令[*]经x=PY变换后，二次型f=XTAX化为[*]
解析：[考点] 含参数的二次型经正交变换化为标准形，求参数及正交变换