问题
单项选择题
设
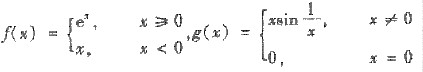
下列四个命题:
(i)在[-1,1]上f(x)存在原函数
(ii)在[-1,1]上f(x)存在定积分
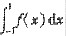
(iii)存在g’(0)
(iV)在[-1,1]上g(x)存在原函数
正确的是 ( )
答案
参考答案:C
解析:[考点] 导数存在,原函数存在,定积分存在的概念
[答案解析] f(x)在[-1,1]上有界,且仅有一个第一类间断点x=0(f(0-)=0≠1=f(0+)).故定积分[*]存在;
[*]在[-1,1]上连续,故在[-1,1]上存在原函数,即(ii)(iV)正确.
又f(x)在x=0不连续,从而不可导,因此f(x)在[-1,1]上不存在原函数,即(i)不正确.又[*]不存在,表明g’(0)不存在,即(iii)不正确.应选(C).
