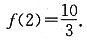问题
问答题
设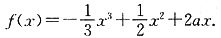
(1)若f(x)在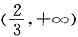 上存在单调递增区间,求a的取值范围;
上存在单调递增区间,求a的取值范围;
(2)当0<a<2时,f(x)在[1,4]上的最小值为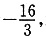 求f(x)在该区间上的最大值.
求f(x)在该区间上的最大值.
答案
参考答案:
(1)f(x)在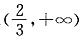 上存在单调递增区间,即存在某个子区间
上存在单调递增区间,即存在某个子区间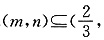 +∞)使得f′(x)>0.由
+∞)使得f′(x)>0.由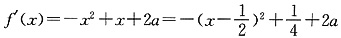 ,f′(x)在区间
,f′(x)在区间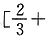 ∞)上存在单调递增区间,则只需
∞)上存在单调递增区间,则只需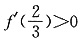 即可,由
即可,由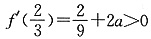 解得
解得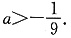
所以,当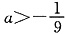 时,f(x)在
时,f(x)在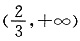 上存在单调递增区间.
上存在单调递增区间.
(2)令f′(x)=0,得两根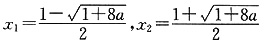
所以f(x)在(-∞,x1),(x2,+∞)上单调递减,在(x1,x2)上单调递增
当0<a<2时,有x1<1<x2<4,所以f(x)在[1,4]上的最大值为f(x2)
又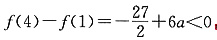 ,即f(4)<f(1)
,即f(4)<f(1)
所以f(x)在[1,4]上的最小值为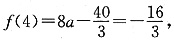 得a=1,x2=2,
得a=1,x2=2,
从而f(x)在[1,4]上的最大值为