问题
问答题
设f(x)=sinx-
(x-t)f(t)dt，其中f为连续函数，求f(x)．
答案
参考答案：所给方程是含有未知函数及其积分的方程．先写成
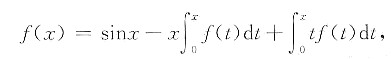
再两边求导，得
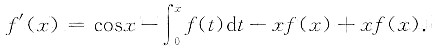
再两边求导，得 f"(x)=sinx-f(x)．
因为①、②都是恒等式，由右边可导可知左边也可导，因而f’(x)，f"(x)是存在的，就是说，f(x)是微方程y"+y=-sinx的解．
特征方程r2+1=0的根为r1，r2=±i，右边的sinx可看作eαxsinβx；α=0，β=1；α±iβ=±i是特征值，因而非齐次方程有特解Y=x·asinx+x·bcosx，代入方程并比较系数，得a=0，b=
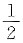，故通解为
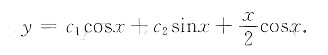
又注意到由①、②，有f(0)=0，f’(0)=1．由此初始条件可确定c1=0，c2=
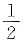，所求函数为f(x)=sinx+
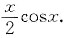
解析：[考点提示] 求微分方程．