问题
问答题
设Г：x=x(t)，y=y(t)(α＜t＜β)是区域D内的光滑曲线，即x(t)，y(t)在区域(α，β)有连续的导数且x’2(t)+y’2(t)≠0，f(x，y)在D内有连续的偏导数。若P0∈Г是f(x，y)在Г上的极值点，求证：f(x，y)在点P0沿Г的切线方向的方向导数为零。
答案
参考答案：主要基于
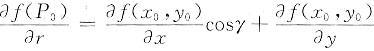sinγ的方向导数计算公式．其中α，γ为切向量的方向角．
当(x，y)∈Г时，f(x，y)变成t的一元函数f[x(t)，y(t)]，记P0对应的参数为t0，即P0为
[x(t0)，y(t0)]=(x0，y0)．
P0是f(x，y)在Г的极值点，即t0是f[x(t)，y(t)]的极值点，于是，由一元函数极值点的必要条件得
f[x(t)，y(t)]是二元函数f(x，y)与一元函数x=x(t)，y=y(t)的复合，由复合函数求导法得
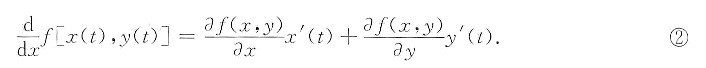
其中：x=x(t)，y=y(t)．注意曲线Г在P0点处的切向量是[x’(t0)，y’(t0)]，单位切向量
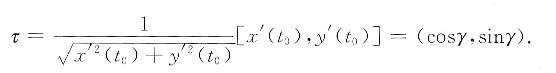
因此，t=t0时，由①、②式得
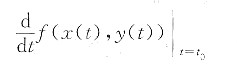
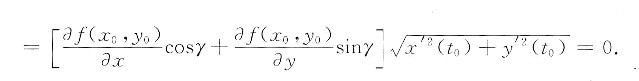
由于
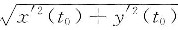≠0及方向导数的计算公式得
解析：[考点提示] 方向导数以及方向向量．