问题
问答题
 (x2+y2+z)dV,其中Ω是由曲线
(x2+y2+z)dV,其中Ω是由曲线
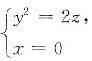 绕z轴旋转一周而成的曲面与平面z=4所围成的立体体积.
绕z轴旋转一周而成的曲面与平面z=4所围成的立体体积.
答案
参考答案:由曲线
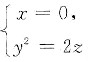 绕z轴旋转一周而成的旋转面方程是x2+y2=2z,于是,Ω是由旋转抛物面z=
绕z轴旋转一周而成的旋转面方程是x2+y2=2z,于是,Ω是由旋转抛物面z=
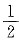 (x2+y2)与平面z=4所围成.曲面与平面的交线是
(x2+y2)与平面z=4所围成.曲面与平面的交线是
x2+y2=8,z=4.
选用柱坐标变换,令x=rcosθ,y=rsinθ,z=z,并选取先rz后θ的积分顺序.极角为θ的半平面与Ω相截得D(θ),于是
Ω:0≤θ≤2π,(r,z)∈D(θ),
D(θ):0≤z≤4,0≤r≤
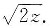
即Ω:0≤θ≤2π,0≤z≤4,0≤r≤
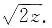
因此
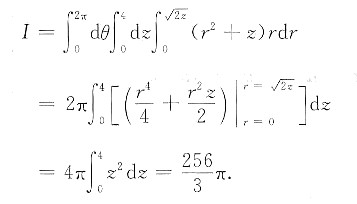
解析:[考点提示] 求旋转曲面的方程.
