问题
问答题
假设曲线l1:y=1-x2(0≤x≤1)与x轴、y轴所围成区域被曲线l2:y=ax2分为面积相等的两部分，其中a是大于零的常数，试确定a的值．
答案
参考答案：如图，由
得曲线l1与曲线l2的交点为
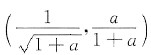，所求平面图形面积为
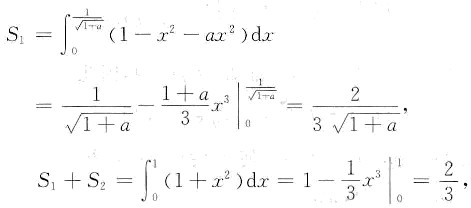
因为S1=S2，所以
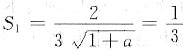，得a=3．
解析：[考点提示] 先求出曲线l1与曲线l2的交点，然后利用定积分求平面图形面积的公式计算出S1和S2．由S1=S2求a的值．
[评注] 本题是利用定积分求面积的基本题型，只是以反问题的形式出现，即已知面积的关系反求参数a，这种出题方式应引起注意．
