参考答案：因为Z=X+Y．所以

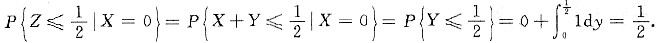
(Ⅱ) 因为Z=X+Y，故随机变量Z的分布函数
F(z)=P{Z≤z}=P{X+Y≤z}．
显然当z≥2时，X，Y的所有取值均满足上式，即F(z)=1；相反当z＜-1时，X，Y只能取空值，则有F(z)=0；而当-1≤z＜2时，

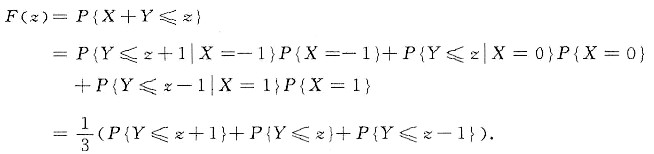
当-1≤z＜0时，

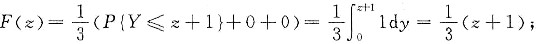
当0≤z＜1时，

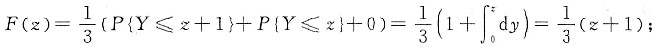
当1≤z＜2时，

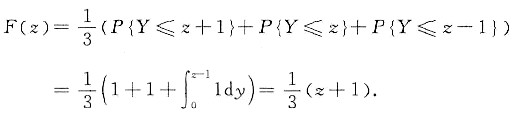
故可得到随机变量Z的分布函数和概率密度分别为

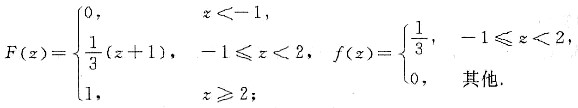
解析：[考点提示] 随机变量的条件概率与概率密度．