问题
问答题
设某产品的成本函数为C=aq2+bq+c，需求函数为
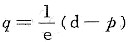．其中C为成本，q为需求量(即产量)，p为单价，a，b，c，d，e都是正的常数，且d＞b．求：
(1) 利润最大时的产量及最大利润；
(2) 需求对价格的弹性；
(3) 需求对价格弹性的绝对值为1时的产量．
答案
参考答案：(1) 利润函数为
L=pq-C=(d-eq)q-(aq2+bq+c)=(d-b))q-(e+a)q2-c．
两边同时对q求导，得
L’=(d-b)-2(e+a)q，
令L’=0，得
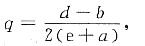
因为L"=-2(e+a)＜0，
所以，当
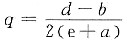时，利润最大，
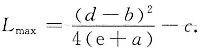
(2) 因为
，所以需求对价格的弹性为
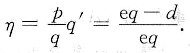
(3) 由|η|=1，得
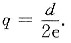
解析：[考点提示] 首先建立各种函数关系，再用导数讨论即可．