问题
问答题
已知3阶矩阵B≠0,且B的每一个列向量都是以下方程组的解:
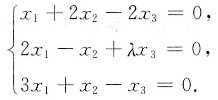
(1) 求λ的值;
(2) 证明|B|=0.
答案
参考答案:
解析:[考点提示] 对于(1),由已知方程组有非零解,得系数行列式|A|=0,可求出λ的值.对于(2),由已知可得AB=0,如|B|≠0,即B可逆,得A=0,这与已知A≠0相矛盾,得|B|=0.
[解题分析] (1)因B≠0.故B中至少有一个非零列向量,依题意,所给齐次方程组有非零解,故必有系数行列式
[*]
由此可得λ=1.
(2) 因B的每一列向量都是原方程的解,故AB=0.
因A≠0则必有|B|=0.事实上,倘若不然,设|B|≠0,则B可逆,故由AB=0两边右乘B-1.得A=0,这与已知条件矛盾,可见必有|B|=0.
