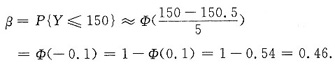问题
问答题
一批产品需要通过检验才能出厂，检验员从产品中任取一件进行检验，取出产品为正品或次品的可能性一样．由于检验误差，一件正品被误判为次品的概率是2%，一件次品被误判为正品的概率是3%．如果一产品经检验被判为次品，那么它无需再进行二次检验；如果检验被判定为正品，那么需要对它再进行二次检验，二次检验均判定为正品的产品才判为正品．假设各次检验是相互独立的，检验员的检验水平不变．
(Ⅰ)试求对一产品进行检验，其检验次数的概率分布；
(Ⅱ)试求经二次检验均判定为正品的产品，它确实为正品的概率α；
(Ⅲ)如果独立地对100个产品进行检验，试应用中心极限定理计算检验总次数不超过150次的概率为β(Ф(0.1)=0.54)．
答案
参考答案：[解答] (Ⅰ)由题设知对一产品进行检验最多检验二次，所以检验次数X可能取值为1，2，且
若记A=“取出产品为正品”，Bi=“第i次检验判定为正品”(i=1，2)．
依题设
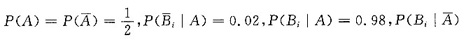
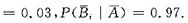
由全概公式得
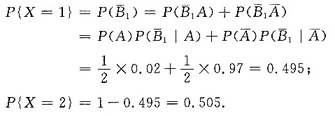
所以检验次数X的概率分布为
[注] ①事件{X=2}=B1=B1B2+
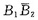，我们也可以应用全概公式计算P{X=2}．
②从上述计算知，第一次检验被判为次品，它确定为次品的概率为
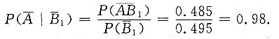
(Ⅱ)
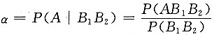，由于各次检验是相互独立的，因此有
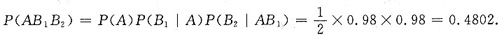
又
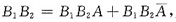应用全概公式得
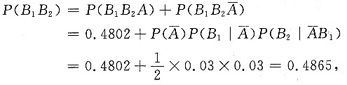
所以
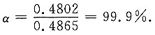
(Ⅲ)若用Xi表示第i个产品检验所需的检验次数，则Xi与X同分布即Xi～
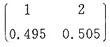，且Xi相互独立(i=1，2，…，100)，EXi=0.495+2×0.505=1.505，EX2i=1×0.495+4×0.505=2.515，DXi=2.515-1.5052=0.25，100个产品检验总次数
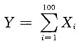，根据独立同分布中心极限定理，Y近似服从正态分布N(EY，DY)=N(150.5，25)，所以
