问题
问答题
设函数f(x)可导，函数g(x)连续，且当f(x)≠0时g(x)可导，求证：
(Ⅰ)当f(x0)≠0时F(x)=|f(x)|g(x)在点x=x0处必可导；
(Ⅱ)当f(x0)=0时F(x)=|f(x)|g(x)在点x=x0处可导的充分必要条件是g(x0)f’(x0)=0．
答案
参考答案：若f(x0)≠0，则存在δ＞0，使得当|x-x0|＜δ时f(x)≠0，于是在该区间内必有|f(x)|g(x)=f(x)g(x)或|f(x)|g(x)=-f(x)g(x)之一成立，故函数|f(x)|g(x)在点x=x0处必可导．
(Ⅱ)若f(x0)=0，于是F(x0)=|f(x0)|g(x0)=0，从而函数F(x)=|f(x)|g(x)在点x=x0的左导数与右导数分别为
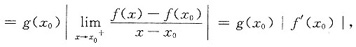
故当f(x0)=0时，
|F(x)|在点x=x0可导
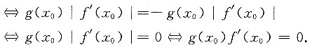
[注] 在上面的证明中用到
与
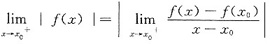，其实更一般地必有
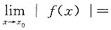
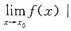.这是因为任何两个数a，b之差与这两个数的绝对值之差成立不等式
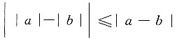，由此即知若
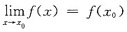必有
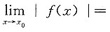
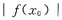，当然对单侧极限也有同样结果．