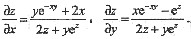问题
问答题
设x=f(x，y)是由方程e-xy-x2+z2+yez=1确定的函数，求
与
．
答案
参考答案：
解法1：公式法——所设的F(x、y、z)中的x，y，z均视为自变量．设F(x，y，z)=e-xy-x2+z2+yex-1，则
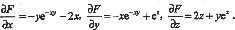所以
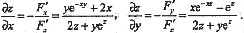
解法2：直接求导——此时x，y是自变量，而z=z(x，y)．等式两边对x求导得
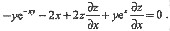等式两边对y求导得
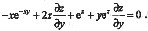解得
搜题请搜索小程序“爱下问搜题”
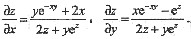
设x=f(x，y)是由方程e-xy-x2+z2+yez=1确定的函数，求与．
参考答案：
解法1：公式法——所设的F(x、y、z)中的x，y，z均视为自变量．设F(x，y，z)=e-xy-x2+z2+yex-1，则
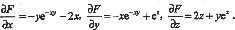所以
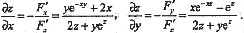
解法2：直接求导——此时x，y是自变量，而z=z(x，y)．等式两边对x求导得
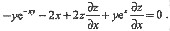等式两边对y求导得
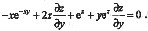解得