问题
问答题
已知f(x)=loga(x+1)，点P是函数y=f(x)图象上任意一点，点P关于原点的对称点Q的轨迹是函数y=g(x)的图象．
(1)当0＜a＜1时，解不等式：2f(x)+g(x)≥0；
(2)当a＞1，x∈[0，1]时，总有f(x)+g(x)≥m恒成立，求m的范围.
答案
参考答案：
设点Q的坐标为(x，y)，由点P、Q关于原点对称，得P点坐标为(-x，-y)
又点P在函数y=f(x)的图象上，∴-y=loga(1-x)
即y=-loga(1-x)得：g(x)=-loga(1-x)
(1)由2f(x)+g(x)≥0得：2loga(x+1)≥log(1-x)
∵0＜a＜1
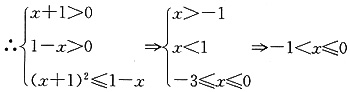
故不等式的解集为(-1，0]
(2)当a＞1，x∈[0，1]时，f(x)+g(x)≥m恒成立，即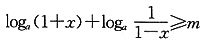
恒成立，也就是
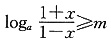在[0，1)上恒成立．设
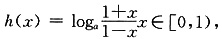则由函数的单调性易知：
h(x)在[O，1)上递增，若使f(x)+g(x)≥m在[0，1)上恒成立，只需h(x)min≥m在[0，1)上成立，即m≤0．
m的取值范围是(-∞，0].
