问题
问答题
一动圆与圆x2+y2+6x+5=0外切，同时与圆x2+y2-6x-91=0内切，求动圆圆心M的轨迹方程，并说明它是什么样的曲线．
答案
参考答案：
设动圆圆心为M(x，y)，半径为R，设已知圆的圆心分别为O1、O2
将圆方程分别配方得：(x+3)2+y2=4，(x-3)2+y2=100
当eM与eO1相切时，有|O1M|=R+2 ①
当eM与eO2相切时，有|O2M|=10-R ②
将①②两式的两边分别相加，得|O1M|+|O2M|=12
即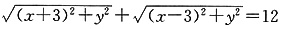
③
移项再两边分别平方得：
④
两边再平方得：3x2+4y2-108=0
整理得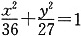
所以，动圆圆心的轨迹方程是
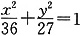，轨迹是椭圆．