某地区冬季干旱，康平社区每天需从外地调运饮用水60吨．有关部门_爱下问搜题

搜题请搜索小程序“爱下问搜题”

问题解答题

某地区冬季干旱，康平社区每天需从外地调运饮用水60吨．有关部门紧急部署，从甲、乙两水厂调运饮用水到供水点，甲厂每天最多可调出40吨，乙厂每天最多可调出45吨．从两水厂运水到康平社区供水点的路程和运费如下表：

	到康平社区供水点的路程（千米）	运费（元/吨·千米）
甲厂	20	4
乙厂	14	5

（1）若某天调运水的总运费为4450元，则从甲、乙两水厂各调运了多少吨饮用水?
（2）设从甲厂调运饮用水x吨，总运费为W元，试写出W关于x的函数关系式，并确定x的取值范围．怎样安排调运方案才能使每天的总运费最省?

答案

（1）从甲、乙两水厂各调运25吨、35吨饮用水；

（2）每天从甲厂调运15吨，从乙厂调运45吨，每天的总运费最省．

题目分析：（1）设从甲厂调运了a吨饮用水，从乙厂调运了b吨饮用水，然后根据题意毎天需从社区外调运饮用水60吨与某天调运水的总运费为4450元列方程组即可求得答案；

（2）首先根据题意求得一次函数W=20×4x+14×5（60﹣x），又由甲厂毎天最多可调出40吨，乙厂毎天最多可调出45吨，确定x的取值范围，则由一次函数的增减性即可求得答案．

试题解析：（1）设从甲厂调运了a吨饮用水，从乙厂调运了b吨饮用水，由题意，得

，

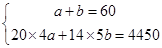解得：．

答：从甲、乙两水厂各调运25吨、35吨饮用水；

（2）设从甲厂调运饮用水x吨，则从乙厂调运（60﹣x）吨，由题意，得

，

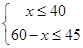解得：15≤x≤40．

W=20×4x+14×5（60﹣x）=10x+4200．

∵k=10＞0，

∴W随x的增大而增大．

∴x=15时，W_最小=4350，

∴每天从甲厂调运15吨，从乙厂调运45吨，每天的总运费最省．

阅读理解与欣赏

阅读下文，完成下面各题。

①科学家认为“甲型H1N1流感”相对温和。尽管世卫组织29日提高了“甲型H1N1流感”疫情警戒级别，而且卫生官员也证实美国出现了首例“甲型H1N1流感”死亡病例，但研究病毒的科学家们却渐渐达成共识，认为目前的混合型流感病毒变种并没有过去引起疫病大流行的那些病毒那么致命。

②事实上，上月底首先在加州圣迭戈和墨西哥南部出现的H1N1病毒变种，主要通过空气和接触传播，其破坏性可能不及每年冬天出现的普通的流感病毒。

③众所周知，流感病毒是不可预测的，这种变种可能在任何时候突变，成为更温和或者更危险的变种，但从基因工程实验室和流行病模型等渠道获得的越来越多的初步证据表明，目前的疫情爆发其最坏的情况可能是可以避免的。

④田纳西州流感病毒学专家理查德？维比说：“这种病毒与1918年的致命性病毒完全没法相比。”

1918年暴发的流感造成全球大约5000万人死亡。

⑤目前的“甲型H1N1流感”病毒首次被查出时，它与1918年的流感病毒相似这一点是不祥之兆。它们都是在春天流感季节的末尾出现，两者似乎都是重点袭击年轻人和健康人，而不是老年人和婴幼儿，而且它们都是H1N1变种，因为他们有着相同的两个关键的蛋白类型，这两个蛋白类型主要决定着病毒的传染力和扩散力。

⑥美国疾病防治中心和国家卫生研究院周一上午公布了加州和德克萨斯州病人身上病毒的基因序列，成千上万的科学家立即开始下载那些信息。他们把病人身上的病毒（1918年的病毒和禽流感病毒

H5N1D等）进行对比，之后发表了令人欣慰的消息。

⑦纽约西纳山医疗中心微生物学家彼得?帕勒斯说：“这种病毒缺少某些特征”。尤其突出的是，这种病毒缺少一种氨基酸。那种氨基酸似乎会导致肺部增生病毒粒子使之更致命。

⑧佐治亚大学流感专家拉尔夫?特里普说，对这种病毒蛋白类型的初步分析表明，经历过1957年那场流感的人可能对这种病毒有一定的免疫力。1957年的那场流感疫情造成全球约200万人死亡。

⑨这或许可以解释墨西哥老年人没有感染上这种病毒的原因。迄今，墨西哥的“甲型H1N1流感”疫情最为严重。（选自《参考消息》2009年5月）

1、科学家提出“甲型H1N1流感”相对温和，下列选项中不能作为依据的一项是[ ]

A．目前的混合型流感病毒变种并没有过去引起疫病大流行的那些病毒那么致命。

B．这种病毒缺少一种氨基酸。那种氨基酸似乎会导致肺部增生病毒粒子使之更致命。

C．H1N1病毒变种主要通过空气和接触传播，其破坏性可能不及每年冬天出现的普通的流感病毒。

D．目前的“甲型H1N1流感”病毒首次被查出时，它与1918年的流感病毒相似这一点是不祥之兆。

2、下列表述不符合文意的一项是 [ ]

A．墨西哥南部出现的H1N1病毒变种的破坏性可能不及每年冬天出现的普通的流感病毒。

B．流感病毒是不可预测的，这种变种可能随时突变，变为更温和或者更危险的变种。

C．“甲型H1N1流感”病毒首次被查出时，人们认为它与1918年的流感病毒完全相同。

D．墨西哥老年人没有感染“甲型H1N1流感”病毒的原因可能是对这种病毒具有一定的免疫力。

3、在第④和第⑤段中，作者使用了哪一种说明方法来解释“甲型H1N1流感”的特征？你觉得使用这种说明方法有什么作用？

。

4、阅读上文和下面两则材料，你能获取哪些信息？

材料一：四川省新闻办公室2009年5月17日下午宣布：与我国内地首例“甲型H1N1流感”患者包某某接触的最后一批人员解除医学观察，患者包某某也同时治愈出院。（《钱江晚报》）

材料二：2009年5月17日，北京确诊一例“甲型H1N1流感”病例，这是我国内地第三例输入性确诊病例。患者为女性，18岁，北京人。5月11日13时50分乘坐美国大陆航空公司C089航班到达北京。北京市卫生部门及时开展了密切接触者的追踪工作，全部密切接触者均已查明并进行了医学观察，未发现不适症状。（《人民日报》）

完形填空

There was a time when I thought my dad didn’t know a thing about being a good father. I couldn’t   31 him ever saying the words “I love you.” It seems to me his only purpose in life was to say “__32_ ” to anywhere I wanted to go and anything I wanted to do, including getting a   33 . Some parents bought their kids cars when they got their driver’s licenses. Not my dad ---- he said that I’d have to get a job and buy my own.
So that is what I did. I got a job at a very nice restaurant and   34  every penny I could and   35 I had enough to buy my car, I did! The day I brought that car home, my dad was the first one I wanted to   36 to. “Look, dad, a car of my own. If you ever want a ride, I’ll only   37 you five dollars.” I offered with a smile.
“I see,” was all he said.
One day, there was something wrong with my father’s truck. So he needed a   38 to work. . The sun wasn’t even up when we left the house,   39  it was already getting warm out. It was going to be a(n)   40 day. As I dropped my dad off, I   41 him, dressed in his work clothes, getting his   42 from the trunk of my car. Watching his sun-weathered face, and even from a distance I could tell there were   43  lines than I ever remembered being there before. I realized how hard my dad works for the family. My father is a cement finisher. In that instant, it   44 to me that he actually got down on his hands and knees to sweat over hot concrete to make a living for his family. And he did this day in and day out,   45 hot it got. Never, not once, had I heard him   46 about it. To him we were “worth” it. And never once did he “charge” us for it.
When he closed the trunk, his tools set off to the side, he walked over to my window to   47 me five dollars. I rolled down the window and said “Good-bye, dad. Keep your five dollars. It’s my   48. Don’t work too hard. I love you.” His   49 met mine, then glanced away in the direction of his waiting tools, he   50 his throat and said, “Oh, and… me, too.”

A．pay it back

B．hand it over

D．show it off