问题
问答题
如图，在三棱柱ABC-A’B’C’中，底面ABC是等腰三角形，AB=BC，∠BAC=30°，
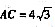，且B’C⊥AC，
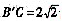，平面B’AC与平面ABC成45°角，A’B与AB’交于点E。
(1)求证：AC⊥BA’；
(2)求异面直线AC与BA’的距离；
(3)求三棱锥B’-BEC的体积。
答案
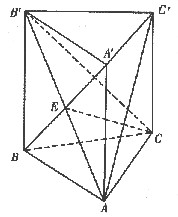
参考答案：
(1)取AC的中点为点D，连接ED。
因为点E是AB’的中点，
所以ED∥B’C，
因为B’C⊥AC，
所以DE⊥AC。
又因为AABC是底角等于30°的等腰三角形，
所以BD⊥AC，BD∩DE=D，
所以AC⊥平面BDE。
所以AC⊥BE．
即AC⊥BA’。
(2)由(1)知∠EDB是二面角B’-AC-B的一个平面角，则∠EDB=45°。
在△ABC中，由得
得EB=[*]
则△BDE是等腰直角三角形。
故ED⊥BE，ED是异面直线AC与BA’的距离，
即异面直线AC与BA’的距离为[*]
(3)连接A’D，则
所以A’D⊥BD。
又因为AC⊥平面BED，A’D[*]平面BED，
所以A’D⊥AC．
所以A’D上平面ABC，且A’D=2。