如图，抛物线关于x轴对称，它的顶点在坐标原点，点P（1，2），A（x1，y1），B（x2，y2）均在抛物线上．
（1）写出该抛物线的方程及其准线方程；
（2）当PA与PB的斜率存在且倾斜角互补时，求直线AB的斜率．
参考答案：
(1)由已知条件，可设抛物线的方程为y2=2px
∵点P(1，2)在抛物线上
∴22=2p×1，得p=2
故所求抛物线的方程是y2=4x，准线方程是x=-1
(2)设直线PA的斜率为kPA，直线PB的斜率为kPB．
则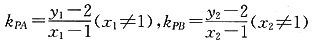
∵PA与PB的斜率存在且倾斜角互补，
∴kPA=-kPB∵A(x1，y1)，B(x2，y2)在抛物线上，得
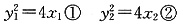
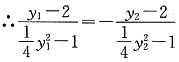∴y1+2=-(y2+2)
∴y1+y2=-4 由①—②得直线AB的斜率
| 阅读以下文字，完成题。 近几年，通信技术网络的超高速化，已成为世界上的发展潮流。空间技术与计算机融合成跨越时间与空间的信息基础结构，它将逐渐深入千家万户，从根本上改变人们的生产、生活和相互交往的方式，加速人类文明和文化的传播，增进相互理解和全球意识。 空间信息的高速公路，这一名词是借鉴信息高速公路概念，也是信息高速公路的拓宽与延伸。所谓空间信息高速公路，我们可以形象地将它理解为以卫星、光纤再辅之以其他通信手段作为“公路”，而以集电脑、电话、传真等为一体的多媒体作为“汽车”，使信息高速传递并能共享的通信网络。这种网络遍布全国乃至全球。在我国则将它称之为国家经济信息化基础设施，其内涵包括4项要素：网络与通信、计算机与信息化设备、信息资源与服务、人与信息化环境。 卫星通信和数字网络光缆就像高速公路一样，是促进社会经济发展的基础设施。它不仅包括地面光缆数字通信网络系统，而且还包括通信卫星、卫星定位系统和环境、灾害监测技术系统。此外．还有不断更新的社会、经济统计数据库和自然资源数据系列，以及宏观调控、规则决策和工程设计服务及知识库，逻辑推理机等人工专家系统，这样，才能有效地实现以信息交流代替人流、物流与能量流。 加速发展空间技术，多方面、高效率利用空间技术，特别是充分利用空间信息资源，促进社会生产力的发展，已成为当今世界的共识。通信卫星具有通信容量大、可靠性高、传输距离远、不受地理环境影响等许多优点，所以备受各国的重视和欢迎。在空间信息高速公路中，卫星无线电信频率宽，极容易实现双向高速率的数据和可视电信业务。并适用于单向多路的电视节目以及新闻报道，对大多数用户都有实用价值。对发展中国家来说，空间信息高速公路的建设，可弥补通信基础设施差与区域性通信空缺之不足。例如，地面信息高速公路的成本昂贵，需要10～15年甚至更长时间才能建成，是一个无法在短期内普及服务的巨额投资项目，而卫星接收设备费用大约只需200美元，其技术是现成的，是一个在短期内能普及并能满足绝大多数用户需求的业务项目。 |
第一段“它将逐步深入千家万户”与第三段“它不仅包括地面光缆数字通信网络系统”两句中的“它”，各指的是( )。
A．都是指空间信息高速公路
B．都是指卫星通信和数字网络光缆
C．前一个“它”指空间信息高速公路，后一个“它”指卫星通信和数字网络光缆
D．前一个“它”指空间技术与计算机融合成跨越时间与空间的信息基础结构，后一个“它”指空间信息高速公路