问题
问答题
设椭圆的轨迹方程为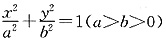 ,焦点分别为F1(-1,0)、F2(1,0),直线l:x=a2交x轴于点A,且
,焦点分别为F1(-1,0)、F2(1,0),直线l:x=a2交x轴于点A,且
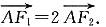
(1)试求椭圆的方程;
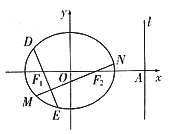
(2)过F1、F2分别作互相垂直的两直线与椭圆分别交于D、E、M、N四点(如图所示),试求四边形DMEN面积的最大值和最小值.

答案
参考答案:
(1)由题意,
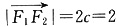 ,且A(a2,0),
,且A(a2,0),
∵
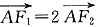 ∴F2为AF1的中点
∴F2为AF1的中点
∴a2=3,b2=2 即:椭圆方程为:
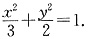
(2)方法一:当直线DE与x轴垂直时,
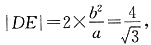 此时
此时
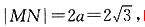 四边形DMEN的面积
四边形DMEN的面积
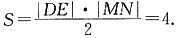 同理当MN与x轴垂直时,也有四边形DMEN的面积
同理当MN与x轴垂直时,也有四边形DMEN的面积
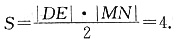 当直线DEMN均与x轴不垂直时,设DE:y=k(x+1),代入消去y得(2+3k2)x2+6k2x+(3k2-6)=0.设
当直线DEMN均与x轴不垂直时,设DE:y=k(x+1),代入消去y得(2+3k2)x2+6k2x+(3k2-6)=0.设
D(x1,y1),E(x2,y2),则
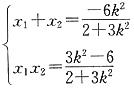
所以,
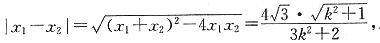 所以,
所以,
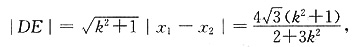 同理
同理
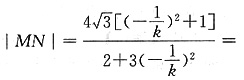
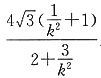 所以四边形的面积
所以四边形的面积
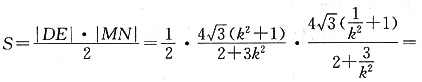
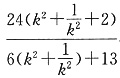 令
令
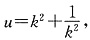 得
得
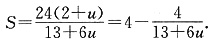 因为
因为
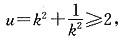 当k=±1时,u=2,
当k=±1时,u=2,
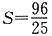 ,且S是以u为自变量的增函数,所以
,且S是以u为自变量的增函数,所以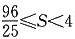
综上可知,
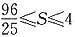 故四边形DMEN面积的最大值为4,最小值为
故四边形DMEN面积的最大值为4,最小值为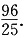
方法二:用直线的参数方程中t的几何意义.
