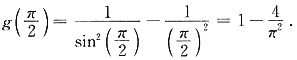问题
问答题
已知函数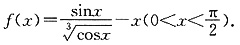
(1)求f(x)的导数f′(x)；
(2)求证：不等式sin3x＞x3cosx在
上恒成立；
(3)
的最大值．
答案
参考答案：
(1)
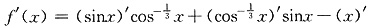
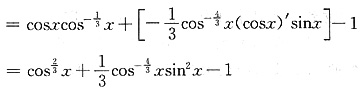
(2)由(1)可知，
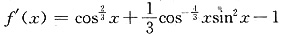，其中f(0)=o．
令f′(x)=G(x)，对G(x)求导得：
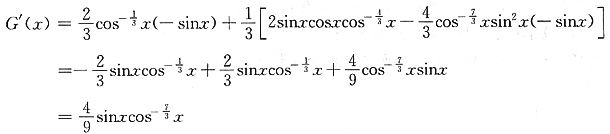
因为G′(x)＞0在
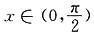上恒成立，所以G(x)即f(x)导函数在
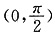上为增函数，故f′(x)＞f′(0)=0．由此可知：
f(x)在
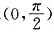上为增函数，故f(x)＞f(0)=0．
当
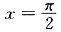时，sin3x＞x3cosx显然成立，所以有sin3x-x3cosx＞0在
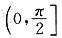上恒成立．
(3)由(2)可知：sin3x-x3cosx＞0在
上恒成立．
则
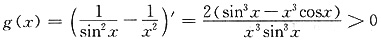在
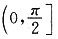上恒成立，即g(x)在
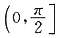上单调递减．
所以当
时，g(x)取得最大值．
