问题
多项选择题
设函数f(x)在[a,b]上满足f"(x)＜0，试证：
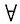x1，x2∈[a,b]，恒有
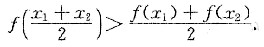
答案
参考答案：证法一 由泰勒公式
[*]
由题设f"(x)＜0，则f"(ξ)＜0，于是有
f(x)＜f(x0)+f’(x0)(x-x0)， ①
对[*]x∈[a,b]的f(x)都成立．
[*]
[*]
证法二 如图B—H—C，因f"(x)＜0，x∈[a,b]，故在[a,b]上函数f(x)的图形上凸，连接曲线y=f(x)(x∈[a,b)上任意两点A(xA，f(xA))，B(xB，f(xB))，得弦[*]的中点为
[*]
由于f(x)的图形上凸，曲线在弦的上方，即点C在点D的上方，因此有
[*]
[*]
解析：
[分析]： 利用泰勒公式或函数图形的凸性证明．