问题
填空题
一动圆与两圆(x+2)2+y2=1,(x-2)2+y2=4都外切,则动圆圆心的轨迹方程为_________________.
答案
=1(x<0)
设动圆圆心P(x,y),则P到(2,0)与P到(-2,0)的距离差是1.∴P点轨迹是以(-2,0)、(2,0)为两焦点,实轴长为1的双曲线的左支.
又∵a=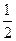
,c=2,∴b2=
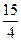.∴=1(x<0)为所求.
搜题请搜索小程序“爱下问搜题”
一动圆与两圆(x+2)2+y2=1,(x-2)2+y2=4都外切,则动圆圆心的轨迹方程为_________________.
=1(x<0)
设动圆圆心P(x,y),则P到(2,0)与P到(-2,0)的距离差是1.∴P点轨迹是以(-2,0)、(2,0)为两焦点,实轴长为1的双曲线的左支.
又∵a=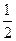,c=2,∴b2=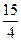.∴=1(x<0)为所求.
