问题
解答题
已知直线l:y=kx-1与双曲线3x2-y2=1交于A、B两点,求弦AB中点P的轨迹方程.
答案
3x2-y2=9(y>1或y≤1).
如右图所示,
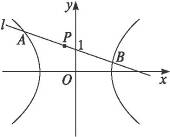
设P(x,y),A(x1,y1),B(x2,y2).
由题意得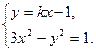
得3x2-(kx-1)2=1,
整理得(3-k2)x2+2kx-2=0.①
则x1、x2是关于x的方程①的两根.
∴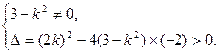
∴k∈(-6,-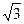 )∪(-
)∪(-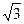 ,
,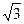 )∪(-
)∪(-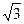 ,
,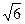 ).
).
又∵x1+x2=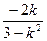 ,∴
,∴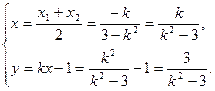
消去k得3x2-y2=9(y>1或y≤1).
