问题
解答题
已知定点A（0，7）、B（0，-7）、C（12，2），以C为一个焦点作过A、B的椭圆，求另一焦点F的轨迹方程.
答案
点F的轨迹方程是y2-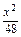
=1(y≤-1)
设F（x，y）为轨迹上的任意一点，
∵A、B两点在以C、F为焦点的椭圆上，
∴|FA|+|CA|=2a，|FB|+|CB|=2a（其中a表示椭圆的长半轴长），
∴|FA|+|CA|=|FB|+|CB|，
∴|FA|-|FB|=|CB|-|CA|
=
-
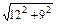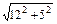=2.
∴|FA|-|FB|=2.
由双曲线的定义知，F点在以A、B为焦点，2为实轴长的双曲线的下半支上，
∴点F的轨迹方程是y2-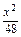=1(y≤-1).