问题
问答题
设函数f(x)在[a，+∞)内二阶可导且f"(x)＜0，又b＞a，f(a)=A＞0，f(b)=B＞0，f’(b)＜0，求证：
(Ⅰ)
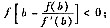
(Ⅱ)方程f(x)=0在[a，+∞)内有且仅有一个实根.
答案
参考答案：[证明] (Ⅰ)方法1°
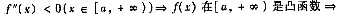
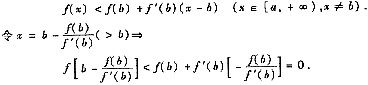
方法2°由泰勒公式可得
+∞)有一个零点.
搜题请搜索小程序“爱下问搜题”
设函数f(x)在[a，+∞)内二阶可导且f"(x)＜0，又b＞a，f(a)=A＞0，f(b)=B＞0，f’(b)＜0，求证：
(Ⅰ)
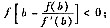
(Ⅱ)方程f(x)=0在[a，+∞)内有且仅有一个实根.
参考答案：[证明] (Ⅰ)方法1°
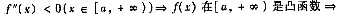
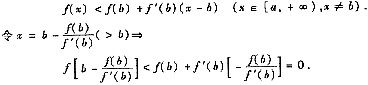
方法2°由泰勒公式可得
+∞)有一个零点.