问题
问答题
.
答案
参考答案：由矩阵A的特征多项式
得到属于λ3=a+1的特征向量α3=k3(2-a，-4a，(a+2)T，k3≠0．
如果λ1，λ2，λ3互不相同，即1-a≠a，1-a≠a+1，a≠a+1，即
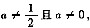则矩阵A有3个不同的特征值，A可以相似对角化，
搜题请搜索小程序“爱下问搜题”
.
参考答案：由矩阵A的特征多项式
得到属于λ3=a+1的特征向量α3=k3(2-a，-4a，(a+2)T，k3≠0．
如果λ1，λ2，λ3互不相同，即1-a≠a，1-a≠a+1，a≠a+1，即
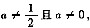则矩阵A有3个不同的特征值，A可以相似对角化，