问题
填空题
[说明]
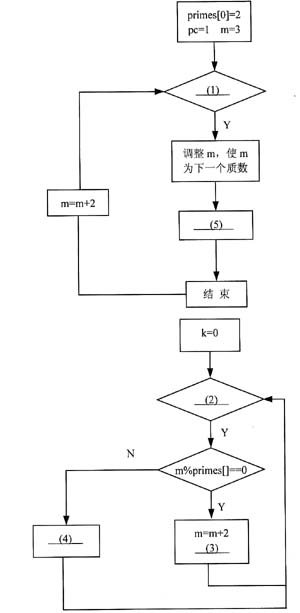
下面的流程图用来说明如何利用数组求前n个质数。要确定一个数m是否是质数,可以用已知求出的质数对m的整除性来确定,对于任意整数m,如果它不能被小于它的质数整除,则m也是质数。
注:primes[]是质数表,已经求得的质数的个数为pc。
[问题]
将流程图的(1)~(5)处补充完整。
答案
参考答案:primes[pc++]=m;
解析: 本题考查的是流程图。
通过阅读流程图,我们可以大致判断出该流程图的思路。首先我们要求的是前n个质数,所以就要判断已经求得的质数的个数pc是否已经为n个,即空(1)应该填入pc<no如果小于n,那么进入下一步的判断,即进入了子流程图。子流程图的功能是:调整m,使m成为下一个质数,在进行完这个步骤后,得到的m就是下一个质数,所以空(5)应该填入primes[pctt]=m。在子流程图中,主要任务是找到另一个质数,可以用已知求出的质数对m的整除性来确定,对于任意整数m,如果它不能被小于它的质数整除,则m也是质数,所以空(2)应该填入m<primes[pc-1]*primes[pc-1]。然后开始判断m是否能被primes[k]整除。如果可以,则说明它不是质数,那么m加2,从k=1开始,进行下一次判断,即空(3)填入k=1。如果m不能被primes[k]整除,那么判断m能否被下一个primes[k]整除,即空(4)填入k=k+1。
