设某二叉树的前序遍历序列为:ABCDEFGGI,中序遍历序列为:BCAEDGHFI
(1)试画出该二叉树;
(2)写出由给定的二叉树的前序遍历序列和中序遍历序列构造出该二叉树的算法。
(3)设具有四个结点的二叉树的前序遍历序列为abcd;S为长度等于4的由a,b,c,d排列构成的字符序列,若任取S作为上述算法的中序遍历序列,试问是否一定能构造出相应的二叉树为什么试列出具有4个结点二叉树的全部形态及相应的中序遍历序列。
参考答案:(1)
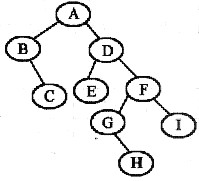
(2)设二叉树的前序遍历序列为P1,P2,…,Pm,中序遍历序列为S1,S2,…,Sm。因为前序遍历是“根左右”,中序遍历是“左右根”,则前序遍历序列中第一个结点是根结点(P1)。到中序序列中查询到Si=P1,根据中序遍历时根结点将中序序列分成两部分的原则,有:
若i=1,即S1=P1,则这时的二叉树没有左子树;否则,S1,S2,…,Si-1是左子树的中序遍历序列,用该序列和前序序列P2,P3,…,Pi去构造该二叉树的左子树。
若i=m,即Sm=P1,则这时的二叉树没有右子树;否则,Si+1,Si+2,…,Sm是右子树的中序遍历序列,用该序列和前序序列中Pi+1。,Pi+2,…,Pm,去构造该二叉树的右子树。算法描述请参见下面算法设计第56题。
(3)若前序序列是abcd,则并非由这4个字母的任意组合(4!=24)都能构造出二叉树。因为以abcd为输入序列,通过栈只能得到1/(n+1)*2n!/(n!*n!)=14种,即以abcd为前序序列的二叉树的数目是14。任取以abcd作为中序遍历序列,并不全能与前序的abcd序列构成二叉树,例如中序序列dcab。
