数据结构DEAP的定义如下:DEAP是一棵完全二叉树,它或者是一棵空树,或者满足下列特性:
(1)树根不包含元素。
(2)其左子树是一小堆(MINHEAP),其右子树是一大堆(MAXHEAP)。
(3)若右子树非空,设i是左子树的任一结点,j是右子树中与i相应的结点,若这样的j结点不存在,则取j为右子树中与i的父结点相应的结点;结点i的关键字总值是小于或等于结点j的关键字值。
一个DEAP的例子如右图所示,与结点15相对应的结点为20,与结点19相对应的结点为25。
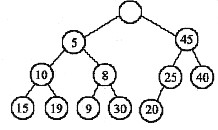
(1)给出在该DEAP中插入结点4后的结果。
(2)写出在DEAP中插入新结点的算法。
(3)编写实现上述算法的程序。
参考答案: DEAP是一棵完全二叉树,树根不包含元素,其左子树是一小堆(MINHEAP,下称小堆),其右子树是一大堆(MAXHEAP,下称大堆),故左右子树可分别用一维数组l[]和r[]存储,用m和n分别表示当前两完全二叉树的结点数,左右子树的高度差至多为1,且左子树的高度始终大于等于右子树的高度。
我们再分析插入情况:当均为空二叉树或满二叉树(m=2h-1)时,应在小堆插入;小堆满(二叉树)后在大堆插入。即当m>=n且m<>2h-1且Llog2m」—LIog2n」<=1时,在小堆插入,否则在大堆插入。
最后分析调堆情况:在小堆m处插入结点x后,若x的值不大于大堆的m/2结点的值,则在小堆调堆;否则,结点x与大堆的m/2结点交换,然后进行大堆调堆。在大堆n处插入结点x后,若x不小于小堆的n结点,则在大堆调堆;否则,结点x与小堆的n结点交换,然后进行小堆调堆。
(1)在DEAP中插入结点4后的结果如图:
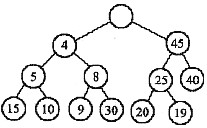
4先插入到大堆,因为4小于小堆中对应位置的19,所以和19交换。交换后只需调整小堆,从叶子到根结点。这时,大堆不需调整,因为插入小堆19时,要求19必须小于对应大堆双亲位置的25,否则,要进行交换。
void InsertDEAP(int 1[],r[],m,n,x)
∥在DEAP中插入元素x,1[]是小堆,r[]是大堆,m和n分别是两堆的元素个数,
x是待插入元素。
{
if(m>=n&&m<>2h-l&&
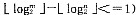 ∥在小堆插入x,h是
∥在小堆插入x,h是
二叉树的高度
m++;∥m增1
if(x>r[m/2])∥若x大于大堆中相应结点的双亲,则进行交换
{
l[m]=r[m/2];
c=m/2;
f=c/2:
while(f>0&&r[f]<x)∥调大堆
{
r[c]=r[f];
c=f:
f=c/2:
}
r[c]=X;
} ∥结束调大堆
else ∥调小堆
{
c=m:
f=c/2:
while(f>0&&[f]>x)
{
l[c]=l[f];
c=f:
f=c/2;
}
l[c]=x;
}
else∥在大堆插入X
{
n++; ∥n增1
if(x<1[n]) ∥若x小于小堆中相应结点,则进行交换
{
r[n]=l[n];
c=n:
f=c/2:
while(f>0&&[f]>x)∥调小堆
{
l[c]=l[f];
c=f:
f=c/2;
}
l[c]=X;
} ∥结束调小堆
else∥调大堆
{
c=n:
f=c/2:
while(f>0&&r[f]<x)
{
r[c]=r[f];
c=f:
f=c/2;
}
r[c]=x;
}
}
