问题
问答题
设f(0)=0,0<f’(x)<1,比较
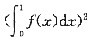 与
与
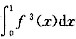 的大小,并证明你的结论.
的大小,并证明你的结论.
答案
参考答案:[详解] 令[*],则F(0)=0.
[*]
因为f(0)=0,0<f’(x)<1,所以f(x)≥f(0)=0.
再令[*],则G(0)=0.
G’(x)=2f(x)-2f(x)f’(x)=2f(x)(1-f’(x))≥0,
∴G(x)单增,∴当x>0时G(x)≥0,∴F’(x)≥0,∴F(x)≥0(x>0).
即[*]
[*]
解析:
[分析]: 构造辅助函数[*]用单调性进行证明.
[评注] 对于常数不等式或定积分不等武,经常将某常数改成x(本题中将1改成x),然后用单调性进行证明.

