问题
问答题
设函数f(x,y)可微,且
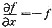 ,
,
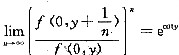 ,
,
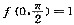 ,求f(x,y).
,求f(x,y).
答案
参考答案:[详解] 因为f(x,y)可微,所以偏导数存在,由偏导数定义得
[*]
即[*],两边对y积分得lnf(0,y)=lnsiny+lnC,
即f(0,y)=Csiny,又[*],得f(0,y)=siny.
由[*],得[*],两边对x积分,
得lnf(x,y)=-x+InC(y),即f(x,y)=C(y)e-x,
代入f(0,y)=siny,得C(y)=siny,所以,f(x,y)=e-xsiny.
解析:
[分析]: 首先利用偏导数定义及1∞型极限得到偏导数方程,再通过积分得到函数.
[评注] 本题属于已知关于偏导数的方程,通过积分求函数.其中综合了偏导数定义以及1∞型极限的求解技巧.
