设三阶实对称矩阵A的特征值为0,1,1,a1,a2是A的两个不同的特征向量,且A(α1+α2)=α2.
(1)证明:
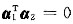 ;
;
(2)求方程组Ax=α2的通解.
参考答案:[详解] 如果α1与α2都是A的属于特征值0的特征向量,
则A(α1+α2)=Aα1+Aα2=0,与A(α1+α2)=α2≠0相矛盾.
同理,如果α1与α2都是A的属于特征值1的特征向量,也会出现矛盾.
如果α1是A的属于特征值1的特征向量,α2是A的属于特征值0的特征向量,
则有A(α1+α2)=Aα1+Aα2=α1与A(α1+α2)=α2相矛盾.
所以,α1是A的属于特征值0的特征向量,α2是A的属于特征值1的特征向量.
(1)因为A是对称矩阵,所以,不同特征值所对应的特征向量必正交,有[*]
(2)因为A是对称矩阵,所以存在可逆阵P,使[*]
因为矩阵[*]的秩为2,故A的秩为2,
所以,齐次方程组Ax=0的基础解系包含一个解向量.
又Aα1=0,Aα2=α2,所以α1是齐次方程组Ax=0的基础解系,α2是方程组Ax=α2的一个特解,所以方程组Ax=α2的通解为kα1+α2.
解析:
[分析]: 首先,由特征值与特征向量的定义及A(α1+α2)=α2,可得α1是A的属于特征值0的特征向量,α2是A的属于特征值1的特征向量.其次,利用对称矩阵的性质及线性方程组的解的结构即可得到结论.
[评注] 对于抽象的矩阵,经常利用定义与性质讨论其特征值与特征向量问题.对于抽象的线性方程组,经常利用线性方程组解的性质与结构定理讨论解的问题.