问题
解答题
设点M在正三角形三条高线上的射影分别是M1，M2，M3（互不重合）．求证：△M1M2M3也是正三角形．
答案
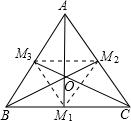
如图所示，
∵△ABC是等边三角形，AM1⊥BC，BM2⊥AC，CM3⊥AB，
∴M1、M2、M3分别是BC，AC，AB的中点，
∴M1M2、M2M3、M1M3是△ABC的中位线，
∴M1M2=M2M3=M1M3=
AB，1 2
∴△M1M2M3是正三角形．
搜题请搜索小程序“爱下问搜题”
