问题
解答题
已知椭圆C中心在原点、焦点在x轴上，椭圆C上的点到焦点的最大值为3，最小值为1．
（Ⅰ）求椭圆C的标准方程；
（Ⅱ）若直线l：y=kx+m（k≠0）与椭圆交于不同的两点M、N（M、N不是左、右顶点），且以MN为直径的圆经过椭圆的右顶点A．求证：直线l过定点，并求出定点的坐标．
答案
解：（Ⅰ）设椭圆的长半轴为a，半焦距为c，
则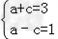
解得
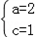
∴椭圆C的标准方程为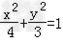
．
（Ⅱ）由方程组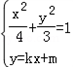
消去y，得（3+4k2）x2+8kmx+4m2﹣12=0
由题意：△=（8km）2﹣4（3+4k2）（4m2﹣12）＞0
整理得：3+4k2﹣m2＞0
①设M（x1，y1）、N（x2，y2），
则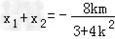
，
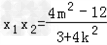
由已知，AM⊥AN，且椭圆的右顶点为A（2，0）
∴（x1﹣2）（x2﹣2）+y1y2=0
即（1+k2）x1x2+（km﹣2）（x1+x2）+m2+4=0
也即
整理得：7m2+16mk+4k2=0
解得：m=﹣2k或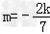
，均满足①
当m=﹣2k时，直线l的方程为y=kx﹣2k，过定点（2，0），舍去
当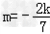
时，直线l的方程为
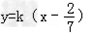，过定点
，
故直线l过定点，且定点的坐标为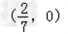
．