问题
解答题
已知椭圆的中心在原点,一个焦点是F(2,0),且两条准线间的距离为λ(λ>4)。
(1)求椭圆的方程;
(2)若存在过点A(1,0)的直线l,使点F关于直线l的对称点在椭圆上,求λ的取值范围。
答案
解:(1)设椭圆的方程为
由条件知c=2,且
所以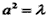 ,
,
故椭圆的方程是 。
。
(2)依题意,直线l的斜率存在且不为0,记为k,则直线l的方程是y=k(x-1)
设点F(2,0)关于直线l的对称点为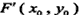
则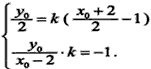 ,解得
,解得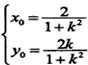
因为点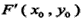 在椭圆上
在椭圆上
所以
即
设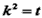
则
因为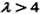
所以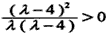
于是,当且仅当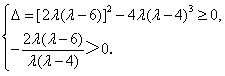 (*)
(*)
上述方程存在实根,即直线l存在
解(*)得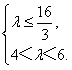
所以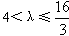 。
。
