问题
问答题
设3阶矩阵
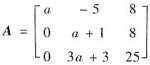，且r(A) ＜3，并已知矩阵B有3个特征值λ1=1，λ2=-1，λ3=0，对应的特征向量分别为
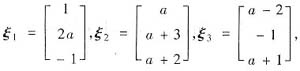
求参数a的值，并求矩阵B．
答案
参考答案：由r(A)＜3，知|A|=0，即有
[*]，即a(a+1)=0．
所以a=0或a=-1．
由于矩阵B有3个互异的特征值，则B应陔有3个线性无关的特征向量，于是B相似于对角阵．
当a=-1时，[*]，所以ξ1，ξ2，ξ3线性相关，故a=-1应舍去．
当a=0时，[*]，由于|ξ1，ξ2，ξ3|=-1≠0，故ξ1，ξ2，ξ3线性无关，所以应取a=0．
由于B相似于对角阵，则[*]，故
[*]