问题
问答题
设二次型
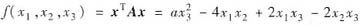，其中二次型矩阵A有特征值4．
试用正交变换将二次型f化为标准形，并写出所用坐标变换；
答案
参考答案：二次型f的矩阵[*]，由λ=4是矩阵A的特征值，有
[*]
所以a=3．
由矩阵A的特征多项式
[*]
得到矩阵A的特征值为λ1=1，λ2=4，λ3=-2．
对于λ=1，由(E-A)x=0，[*]
得到矩阵A属于λ=1的特征向量α1=(-1，1，1)T．
对于λ=4，由(4E-A)x=0，
[*]
得到矩阵A属于λ=4的特征向量α2=(1，-1，2)T．
对于λ=-2，由(-2E-A)x=0，
[*]
得到矩阵A属于λ=-2的特征向量α3=(1，1，0)T．
由于α1，α2，α3已两两正交，故只需单位化，有
[*]
那么，令
[*]
在正交变换x=Qy下，有
[*]
二次型[*]．