问题
问答题
求一正交变换,将二次型
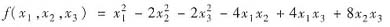
化为标准形,并指出f(x1,x2,x3)=1表示何种二次曲面.
答案
参考答案:二次型的矩阵为[*],由
|λE-A|=(λ-2)2(λ+7),
得A的特征值为λ1=λ2=2,λ3=-7.
可求得对应λ1=A,=2的特征向量为α1=(-2,1,0)T,α2=(2,0,1)T.
将其正交化 β1=α1=(-2,1,0)T,
[*]
再单位化
[*]
又矩阵A对应λw=-7的特征向量为α3=(-1,-2,2)T,单位化得[*],故经正交变换
[*]
化二次型为标准形[*].
可知f(x1,x2,x3)=1表示旋转单叶双曲面.
