问题
问答题
设A是4阶矩阵,λ=0是A的三重特征值,
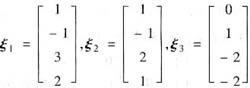 是A的对应于λ=0的特征向量.
是A的对应于λ=0的特征向量.
问
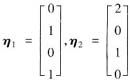 是否也是A的对应于λ=0的特征向量,说明理由;
是否也是A的对应于λ=0的特征向量,说明理由;
答案
参考答案:因
[*]
于是r(ξ1,ξ2,ξ3)=3,故ξ1,ξ2,ξ3线性无关.
由于λ=0是A的三重特征值,对应的线性无关的特征向量不超过3个,现已知ξ1,ξ2,ξ3是3个对应的特征向量,故若η1,η2也是A的对应于λ=0的特征向量,则η1,η2必可由ξ1,ξ2,ξ3线性表出.但
[*]
[*]
由于 r(ξ1,ξ2,ξ3,η1)=4≠r(ξ1,ξ2,ξ3)=3,
r(ξ1,ξ2,ξ3,η2)=4≠r(ξ1,ξ2,ξ3)=3,
故η1,η2都不能由ξ1,ξ2,ξ3线性表出,也就都不是A的对应于λ=0的特征向量.
