问题
问答题
已知n阶非零矩阵A1，A2，A3满足
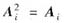(i=1，2，3)，AiAj=0 (i≠j，i，j=1，2，3)．
证明：Ai属于λ=1的特征向量是Aj属于λ=0的特征向量(i≠j)；
答案
参考答案：若Aiα=α，α≠0，两边用Aj左乘，得
Ajα=AjAiα=0α=0=0α．
故α是Aj属于λ=0的特征向量．
搜题请搜索小程序“爱下问搜题”
已知n阶非零矩阵A1，A2，A3满足
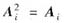(i=1，2，3)，AiAj=0 (i≠j，i，j=1，2，3)．
证明：Ai属于λ=1的特征向量是Aj属于λ=0的特征向量(i≠j)；
参考答案：若Aiα=α，α≠0，两边用Aj左乘，得
Ajα=AjAiα=0α=0=0α．
故α是Aj属于λ=0的特征向量．