问题
问答题
设f（x，y，z）=xy2z3，且z=z（x，y）由方程x2+y2+z2-3xyz=0确定，求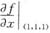
．
答案
参考答案：
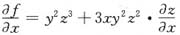
方法一 用公式法求
设F(x，y，z)=x2+y2+z2-3xyz，则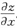
，
所以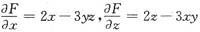
因此有
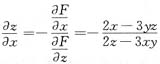
所以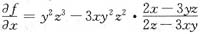
方法二 用微分法求．
对等式x2+y2+z2-3xyz=0求微分得
2xdx+2ydy+2zdz-3yzdx-3xzdy-3xydz=0．
解得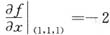
比较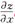
可得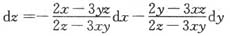
，下同方法一略．
解析：
本题考查的知识点是隐函数求偏导．隐函数求偏导常用的有两种方法：公式法和微分法．直接求导的计算量比较大，建议考生熟练掌握公式法．首先应求出，此时的z=z(x，y)是隐函数，需用隐函数求偏导的方法求出．