问题
填空题
设矩阵
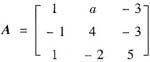 不可对角化,且其特征值有重根,则a=______.
不可对角化,且其特征值有重根,则a=______.
答案
参考答案:F
解析:
[分析]: 由A的特征多项式
[*]
=(λ-2)(λ2-8λ+10+a),
若λ=2是重根,则λ2-8λ+10+a中含有λ-2的因式.令g(λ)=λ2-8λ+10+a,即有g(2)=0,因此有22-8×2+10+a=0,解得a=2.此时
|λE-A|=(λ-2)2(λ-6),
A的3个特征值分别为λ1=λ2=2,λ3=6,当λ=2时(二重),r(2E-A)=1,故对应于λ=2有两个线性无关的特征向量.因此,A可对角化.
若λ=2不是A的重特征值时,则λ2-8λ+10+a是完全平方式,即有10+a=16,解得a=6.此时
|λE-A|=(λ-2)(λ-4)2,
A的3个特征值分别为λ1=2,λ2=λ3=4.当λ=4时(二重),r(4E-A)=2,故对应于λ=4只有一个线性无关的特征向量,因此A不可对角化.
综上分析,a=6.
