问题
问答题
已知矩阵
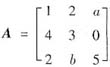，有3个线性无关的特征向量，λ=5是矩阵A的二重特征值，A*是矩阵A的伴随矩阵，求可逆矩阵P，使P-1A*P为对角矩阵．
答案
参考答案：因为矩阵A有三个线性无关的特征向量，λ=5是矩阵A的二重特征值，故矩阵A属于特征值λ=5必有2个线性无关的特征向量，因此秩r(5E-A)=1．由
[*]
得a=0，b=-1．又由
5+5+λ3=1+3+5，
知矩阵A的特征值是λ1=λ2=5，λ3=-1．
那么，|A|=-25，伴随矩阵A*的特征值是-5，-5，25．
由齐次方程组(5E-A)x=0，得基础解系α1=(1，2，0)T，α2=(0，0，1)T，它是矩阵A属于特征值λ=5的线性无关的特征向量，亦是A*属于特征值λ=-5的线性无关的特征向量．
由齐次方程组(-E-A)x=0，得基础解系α3=(-2，2，1)T，它是矩阵A属于特征值λ=-1的特征向量，亦是A*属于特征值λ=25的特征向量．
那么，令[*]，有[*]