问题
问答题
设A是3阶矩阵,λ0是A的特征值,对应的特征向量为ξ=(1,1,1)T,已知|A|=1,又A*是A的伴随矩阵,且
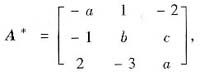
试确定参数a,b,c及λ0.
答案
参考答案:由题设条件知Aξ=λ0ξ,两边左乘A*,且利用|A|=1,得
A*Aξ=|A|ξ=ξ=λ0A*ξ.
代入A*,ξ,得
[*]
即[*]
因|A|=1,故λ0≠0,由方程①、③得
-a-1=-1+a,得a=0.
由a=0代入①式,得λ=-1,代入②得
1-b-c=1,即b+c=0.
于是[*].因|A|=1,故|A*|=|A|3-1=1,从而有
[*]
得[*]
从而有a=0,[*]
