问题
填空题
f(x1，x2，x3，x4)=
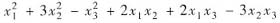的矩阵A=______
(Ⅱ)
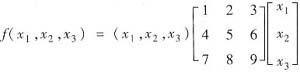的矩阵A=______；
(Ⅲ)f(x1，x2，x3)=(ax1+bx2+cx3)2的矩阵A=______．
答案
参考答案：[*]，[*]，[*]
解析：
[分析]： (Ⅰ)应注意由f(x1，x2，x3，x4)可知右端的二次型为4元二次型，虽然二次型右边表达式中没有含x4的项，但其对应矩阵必须补零做成4阶对称矩阵，即
[*]
(Ⅱ)尽管题中二次型写成了矩阵形式，但所给的矩阵不是对称矩阵，因此需要先展开二次型，再写二次型的矩阵，即
[*]
故二次型矩阵为
[*]
(Ⅲ)将右端三项式展开，再写二次型的矩阵较烦．如先将三项式ax1+bx2+cx3写成两矩阵相乘的形式，计算较简单．
f(x1，x2，x3)=(ax1+bx2+cx3)2=(ax1+bx2+cx3)(ax1+bx2+cx3)
[*]
故二次型矩阵为
[*]