问题
填空题
设
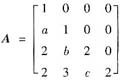 可对角化,则a,b,c的取值为______.
可对角化,则a,b,c的取值为______.
答案
参考答案:a=c=0,b任意
解析:
[分析]: |λE-A|=(λ-1)2(λ-2)2,所以A的特征值为λ1=λ2=1,λ3=λ4=2.为使A可对角化,则A对应二重特征值1和2应分别有2个线性无关的特征向量,即r(E-A)=2,r(2E-A)=2.由于
[*]
可见为使r(E-A)=2,必须a=0,而b,c任意.为使r(2E-A)=2,必须c=0,而a,b任意.故当a=c=0,而b任意时,A可对角化.
